PartialRankerMin

Experiments with finding the partial rank with minimum possible number of ranks. In order to follow, please refer to Methodology 3 in the paper.

Experiment 3

Consider again the data from the previous section for which Methodology2 did not find the partial ranking with the least number of ranks. Recall, 10 objects are created, each with 3 measurement values sampled from 2 different normal distributions that are well-separated.

from partial_ranker import MeasurementsSimulator, MeasurementsVisualizer

n1 = [0.2, 0.02]
n2 = [0.3,0.02]
M5 = {}

for i in range(5):
    M5['t{}'.format(i)] = n1

for i in range(5,10):
    M5['t{}'.format(i)] = n2

ms = MeasurementsSimulator(M5,seed=512)
ms.measure(reps=3)
measurements = ms.get_measurements()

mv = MeasurementsVisualizer(measurements)
fig = mv.show_measurements_boxplots(scale=0.5)

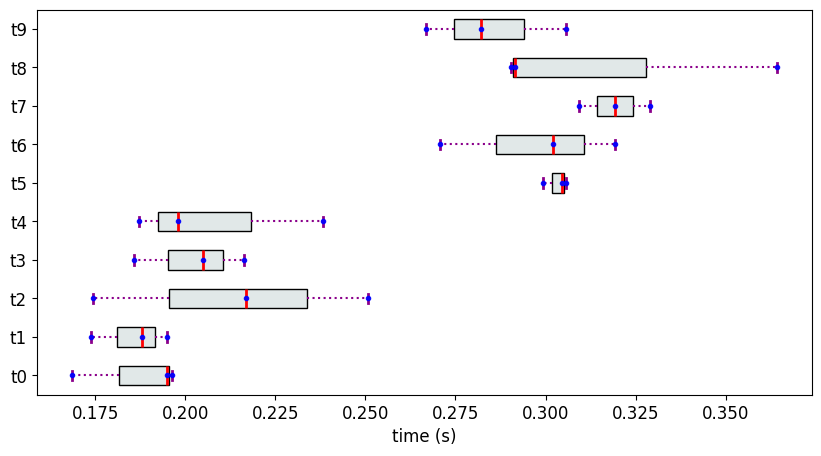
The Partial Ranks according to Methodology 3

from partial_ranker import QuantileComparer, Method,PartialRanker

cm = QuantileComparer(measurements)
cm.compute_quantiles(q_max=75, q_min=25)
cm.compare()
pr = PartialRanker(cm)
pr.compute_ranks(Method.Min)
pr.get_ranks()

{0: {'t0', 't1', 't2', 't3', 't4'}, 1: {'t5', 't6', 't7', 't8', 't9'}}